type
status
date
slug
summary
tags
category
icon
password
前置
- 前缀和(维护区间和)
- 二维前缀和
- 差分
数组(维护区间内加减)(前缀和为原数组)
树状数组
- 单点修改和区间求和
- 区间修改和单点查询
- 区间修改和区间查询
可以用前缀和的方法维护这个数组，这样的话区间求和的时间复杂度就降到了$O(1)$
，但是单点修改会影响后面所有的元素，时间复杂度是$O(n)$。
树状数组的实现
当然是使用树形数据结构了。
利用二进制的性质来维护一棵树
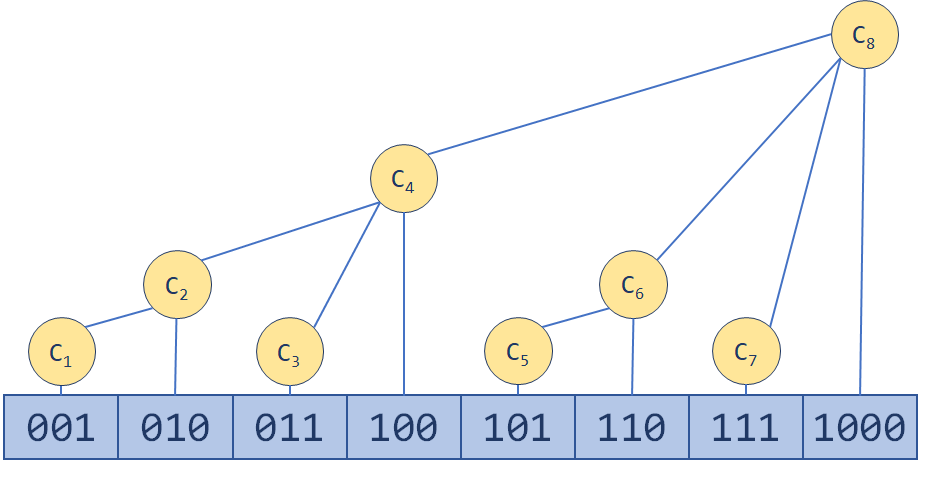
而树的遍历操作使用进制实现：
具体操作为：
区间修改和单点查询：使用差分数组取代原数组即可。
二维树状数组
将树的处理化为二维，
而求值参考二维前缀和的式子
树上前缀和（LAC）
ll
某个节点到根的路径上的每个点的权值和
求法：
时带参数传递下去即可
树上差分
某个节点对它到根的路径上的每个点的贡献
求法：修改
x到y上每个点/边的权值时：
高维前缀和
对于一个二维前缀和，代码可能是这样的
对于更高维的会很麻烦
就用二进制状压简化
二维差分
- Author:Grimner
- URL:https://tangly1024.com/article/example-9
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!